p-q-Formel
Die p-q-Formel ist eine Hilfsformel zum lösen von Quadratischen Formeln. Dazu wird die Quadratische Gleichung in der sogenannten Normalform benötigt.
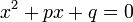
\(x^2 + px + q = 0\)
Nun müssen lediglich die Werte für p und q in die folgende pq-Formel eingesetzt werden.
\(x_{1,2} = -\frac{p}{2} \pm \sqrt{\left(\frac{p}{2}\right)^2 - q}\)
Eine andere Möglichkeit Polynome zweiten Grades zu lösen ist die Mitternachtsformel
Folgende Eselsbrücke wurde zum Thema p-q-Formel gefunden. Für detaillierte Ergebnisse kannst du auch die Suche benutzen. Wenn du auch dort keinen passenden Merksatz bzw. keine passende Eselsbrücke findest, kannst du unser Hier fehlt etwas Formular benutzen, um auf dieses Problem aufmerksam zu machen. Wir werden uns darum kümmern, dass dir schnellstmöglich das Lernen und Merken vereinfacht wird!
Ich habe ein halbes Pferd Schulden (-p/2);
Da es keine halben Pferde geben kann, muss ich mir entweder ein weiteres halbes Pferd dazu leihen, oder das halbe Pferd zurückgeben (Deswegen /- p/2);
das zurückzugebenden/zusätzlich auszuleihende Pferd kann ich quadrieren und gleich danach die Wurzel ziehen, somit bleibt das Ergebnis gleich ( /- sqrt((p/2)^2);
Nun ist es so, dass mir der andere (Bauer) sowieso noch eine Kuh schuldet, die kann ich von meinen Schulden abziehen (-q);
Ich mache das ganze aber zur "Tarnung" geschickt unter der Wurzel... ( /- sqrt((p/2)^2-q));